Page sur une application du théorème de Pythagore

Lors d’un exercice dans le chapitre sur les distances et les tangentes, j’ai essayé de le résoudre à l’aide du théorème de Pythagore, sans succès. L’exercice est assez facile si on travaille avec les outils prévus (tangente, distance, bissectrice et angles d’un triangle) et puisqu’il s’agit de démontrer un angle droit, j’ai pensé conclure avec uniquement le théorème de Pythagore.

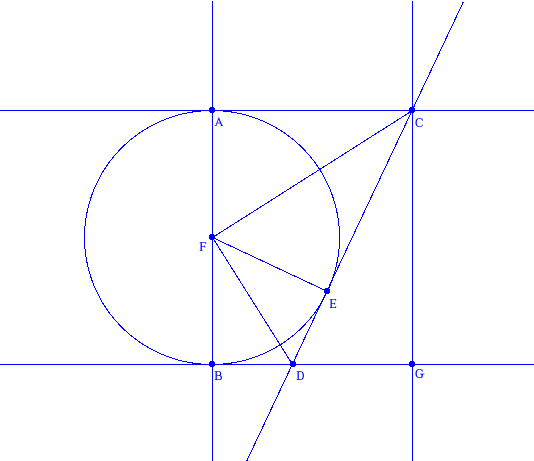
Les droites qui semblent tangentes le sont bien et (AC)⫽(BG), il s’agit de prouver que $\widehat{\mathrm{DFC}}=90\mathrm{°}$. Voici le fichier kig.

Preuve élémentaire

Commençons par prouver le lemme suivant :

Si deux droites tangentes à un même cercle se coupent, alors les deux distances de ce point à chacun des points de contact sont égales.

En d’autres mots, ici on aura BD=DE et AC=CE.

Intéressons-nous au quadrilatère FBDE et aux triangles FBE et BED. FBE est isocèle en F puisque FB=FE (rayons du cercle), donc $\widehat{\mathrm{FBE}}=\widehat{\mathrm{BEF}}$. Comme (BD) et (DE) sont tangentes au cercle, les angles $\widehat{\mathrm{FBD}}$ et $\widehat{\mathrm{FED}}$ sont droits, donc par différence, les angles $\widehat{\mathrm{EBD}}$ et $\widehat{\mathrm{EBD}}$ sont égaux, donc BED est isocèle en D, et en conclusion BD=DE. CQFD.

On aurait pu le démontrer en utilisant les triangles FBD et FED égaux (angles droits, hypoténuses et côtés égaux).

Maintenant démontrons que $\widehat{\mathrm{DFC}}=90\mathrm{°}$.

On a donc montré que (FD) est la bissectrice de $\widehat{\mathrm{BFE}}$, et de même on motre que (FC) est celle de $\widehat{\mathrm{AFE}}$. Donc l’angle plat $\widehat{\mathrm{AFB}}$ est coupé en quatre angles, égaux deux à deux. $\widehat{\mathrm{AFB}}=2\widehat{\mathrm{CFE}}+2\widehat{\mathrm{DFE}}$, donc $\widehat{\mathrm{CFE}}+\widehat{\mathrm{DFE}}=90\mathrm{°}$. DFC est rectangle en F.

Essai avec le théorème de Pythagore

En fait, j’ai essayé de le redémontrer en contournant les résultats élémentaires sur les angles, mais sans succès. Il s’agit de montrer que DF²+FC²=DC².

FED et FEC sont rectangles en E donc en appliquant deux fois le théorème de Pythagore :

DF²+FC²=2 FE²+DE²+EC²=2 FA²+DE²+EC²

Or DC²=(DE+EC)²=DE²+EC²+2×DE×EC

AB²=4 FA²

On identifie DE²+EC² et donc ${\mathrm{DF}}^2+{\mathrm{FC}}^2=\frac{{\mathrm{AB}}^2}{2}+{\mathrm{DC}}^2-2\times \mathrm{DE}\times \mathrm{EC}$ ; remarquez que je viens d’utiliser BD=DE et AC=CE (qui se démontre ici avec le théorème de Pythagore) et que donc tous ces calculs ne servent à pas grand-chose.

${\mathrm{DG}}^2={\left(\mathrm{AC}-\mathrm{BD}\right)}^2={\mathrm{AC}}^2+{\mathrm{BD}}^2-2\times \mathrm{BD}\times \mathrm{DC}$

Essayons de développer FD et FC, hypoténuses des triangles FBD et FAC.

DF²+FC²=2 FA²+BD²+AC²=2 FA²+DG²+2×AC×BD

Il faudrait que DG²+2×AC×BD=DC²−2×DE×EC, c’est-à-dire que CG²=DC²−DG²=2×AC×BD+2×DE×EC, soit 2×FA²=2×AC×BD (DE=BD et EC=AC) donc FA²=AC×BD or les deux quadrilatères ACEF et BDEF sont semblables donc on a bien ce qu’on cherche ; à ceci près qu’on a encore utilisé les égalités d’angles, et donc que tout ce travail aurait pu être écourté.

Dans le même ordre d’idées, on aurait pu utiliser le théorème de Ptolémée dans ACEF et BDEF, qui sont respectivement inscriptibles dans un cercle de diamètre [FC] et [FD] (en plus AC=CE, FA=FE, FE=FB, ED=DB) :

2×FA×AC=AE²+FC² et 2×FE×BD=BD²+FD²

Avec des produits scalaires

$\overrightarrow{\mathrm{FD}}\cdot \overrightarrow{\mathrm{FC}}=\left(\overrightarrow{\mathrm{FB}}+\overrightarrow{\mathrm{BD}}\right)\cdot \left(-\overrightarrow{\mathrm{FB}}+\overrightarrow{\mathrm{AC}}\right)=-{\mathrm{FB}}^2+\underset{\underset{0}{⏟}}{\overrightarrow{\mathrm{FB}}\cdot \overrightarrow{\mathrm{AC}}-\overrightarrow{\mathrm{BD}}\cdot \overrightarrow{\mathrm{FB}}}+\overrightarrow{\mathrm{BD}}\cdot \overrightarrow{\mathrm{AC}}=\mathrm{BD}\times \mathrm{AC}-{\mathrm{FB}}^2$

Ce qui vaut aussi $\left(\overrightarrow{\mathrm{FE}}+\overrightarrow{\mathrm{ED}}\right)\cdot \left(\overrightarrow{\mathrm{FE}}+\overrightarrow{\mathrm{EC}}\right)={\mathrm{FE}}^2+\overrightarrow{\mathrm{ED}}\cdot \overrightarrow{\mathrm{EC}}={\mathrm{FE}}^2-\mathrm{DE}\times \mathrm{EC}$

Comme FE=FB, on retrouve l’égalité trouvée avec le théorème de Ptolémée.

Maison